Projection (System of)
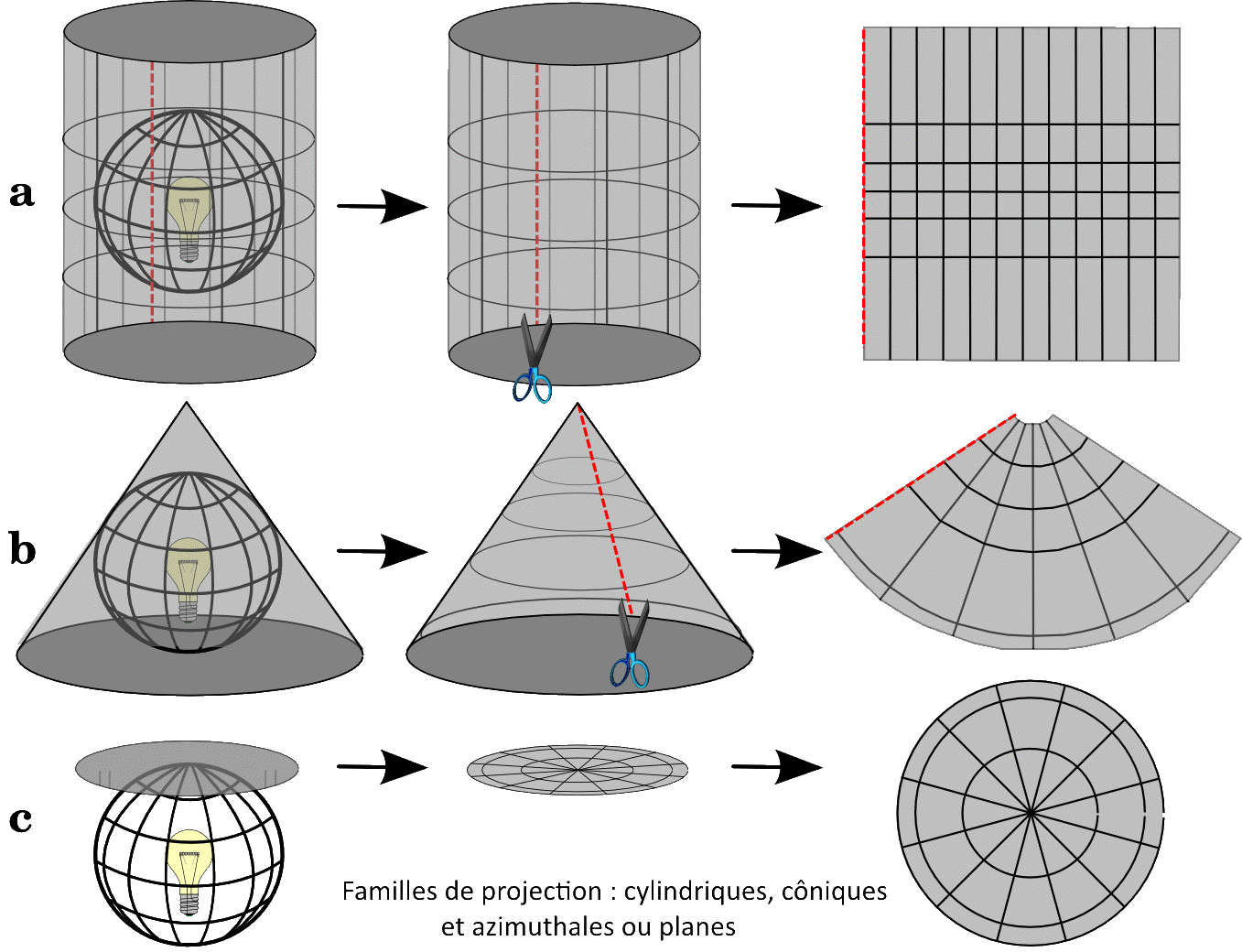
The Earth has an approximately spherical shape, which poses a problem when we want to visualize its surface on a plane, as is the case for a map on paper or a computer screen. This requires several operations to be carried out. We must first develop a model of the irregular volume of the Earth, called a geoid, from which we can build a system or geodetic datum that will precisely locate a point on the surface of the earth. We then create a projection system, a mathematical model to locate any point on the earth's surface on a flat surface. Numerous projection systems have been proposed starting from cylinders, cones …
We can distinguish between several families of projection (source http://docs.qgis.org/2.2/fr/docs/gentle_gis_introduction/coordinate_reference_systems.html#figure-projection-families):
The choice of projection depends on the objectives of the cartographer. Should the angles be respected, and therefore the shapes of objects, but at the expense of the accuracy of the surfaces? Or vice versa, because no projection retains both? What area is to be mapped: a region, a country, a continent? Some systems are better adapted for local areas and others for larger areas. The latitude of the area to be mapped is also to be taken into account.
In metropolitan France, the old NTF geodesic system and the Lambert 4 Zones projections are still used but they must officially be replaced by the RGF 93 system. The official Lambert 93 projection for maps of metropolitan France is now the Lambert 93 projection, or rather a system of 9 projections. Another widely used geodesic system is WGS 84, associated with GPS. A widely used conformal projection is the Universal Transverse Mercator (UTM). Once the parameters of the geodesic system and the projection are known, most GIS software can transform a data set from one projection system to another.