Wiki du Master Géographies Numériques

Cette notion de simplification et de déformation des objets résulte du passage d’une carte à une certaine échelle à une échelle plus petite. Autrement dit, il s’agit de la réduction d’une carte et de son contenu. Ainsi, la généralisation consiste en un changement de niveau d’observation et donc en une réduction du nombre d’objets représentés, ce qui conduit à une modification d’implantation.

Cette schématisation suit deux règles basées sur le principe de la caricature :
- l’amplification et l’exagération des accidents
- la suppression des détails mineurs

La généralisation, par la simplification volontaire de la forme des objets (linéaires ou zonaux), a plusieurs objectifs :
- la suppression des sinuosités
- la suppression des angularités (dont l’amplitude est trop faible)
- l’application de signes conventionnels (tracés routiers jumelés)
- le maintien de la figuration de certains éléments (s’ils sont caractéristiques de l’objet géographiques ou s’ils mettent en évidence des phénomènes essentiels).


Cette opération est possible dans GRASS GIS par la fonction « Vecteur/Outils de topologie/Lisser ou simplifier » ou via la commande « v.generalize ») Après avoir rentré la couche en entrée et celle en sortie, il vous faudra choisir l’algorithme à utiliser pour réaliser la généralisation (menu déroulant « Generalization algorithm ») et renseigner ensuite les paramètres dont il a besoin pour calculer la déformation des objets.



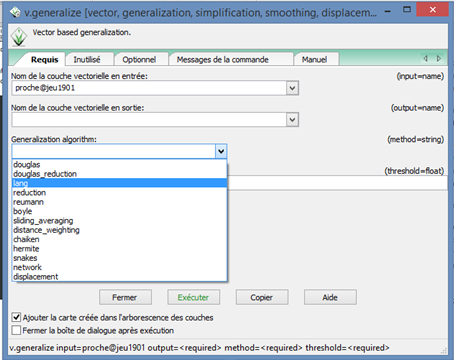
13 choix s’offrent alors à vous suivant le type de simplification recherché :

Algorithmes de simplification des objets

• Douglas: algorithme le plus largement utilisé pour la simplification de lignes. Il nécessite de connaître uniquement les paramètres input et threshold. Pour de plus amples informations sur cette méthode:http://fr.wikipedia.org/wiki/Algorithme_de_Douglas-Peuker
  
  
• Douglas_reduction: ajoute au premier algorithme un paramètre de réduction qui représente le pourcentage de points restants sur la ligne simplifiée par rapport au nombre de points présents sur la ligne d'origine. Les paramètres d'entrée sont les suivants : input, threshold, reduction
  
  
• Lang: autre algorithme standard pour la simplification de lignes. Les paramètres input, threshold et look_ahead sont nécessaires pour appliquer ce calcul.
  
  
• Reduction: algorithme de réduction de sommets (vertex). Il élimine les points proches les uns des autres situés en dessous du paramètre de seuil fixé (threshold) avant le lancement de la simplification.
  
  
• Reumann: algorithme qui permet de préserver les caractéristiques globales des lignes en fonction des paramètres input et threshold.
  
  

Algorithmes de lissage des objets

• Boyle: algorithme qui calcule la position de chaque sommet en fonction de la position du sommet qui le précède et de celui qui lui succède. Ce traitement ne change pas le nombre de points de la ligne. Seuls les paramètres input et look_ahead sont nécessaires.
  
  
• Sliding_averaging: la nouvelle position d’un point est déterminée par la précision du paramètre look_ahead des points qui l’entourent. Le nombre de points ne varie pas. Les paramètres input, slide et look_ahead (dont la valeur doit être impaire et différente de 1) doivent être renseignés pour que cet algorithme soit calculé.
  
  
• Distance_weighting: calcule la nouvelle position d’un sommet à partir de la moyenne pondérée du paramètre look_ahead (dont la valeur doit être impaire et différente de 1) des différents points de la ligne. Le paramètre slide est utilisé pour une interpolation linéaire entre la position d’origine du point et celle nouvellement calculée. Aucun point n’est rajouté à la ligne.
  
  
• Chaiken: calcule une nouvelle position à partir de la ligne d'origine de manière que les points sur cette nouvelle ligne aient le même seuil que sur l'originale. Les paramètres d'entrée sont les suivants : input (couche vecteur en entrée), threshold (seuil).
  
  
• Hermite: Cet algorithme prend les points de la polyligne comme points de contrôle de la « courbe cubique » Hermite et se rapproche de cette courbe par les points qui avoisinent le seuil défini. Cette méthode a d’excellents résultats pour de petites valeurs du seuil mais produit en contrepartie une grande quantité de points. Une simplification antérieure de la ligne est généralement nécessaire avant d’effectuer ce traitement. Un des avantages-clés de l’interpolation d’Hermite est le fait que la ligne calculée passe toujours par les points de la ligne d'origine, tandis que les lignes produites par les autres algorithmes ne passent jamais par ces points. Les paramètres nécessaires sont : input, threshold, angle_thresh.
  
  
• Snakes: Cette méthode conserve les caractéristiques générales des lignes, mais lisse les angles vifs de la ligne. Cet algorithme fonctionne très bien pour de petites valeurs (comprises entre 0 et 5) des paramètres alpha et beta. Ces paramètres affectent la «netteté» et la courbure de la ligne calculée. Cet algorithme n’est pas très efficace pour les lignes constituées de plusieurs segments.
  
  

Généralisation de réseau

• Network: Utilise la part la plus importante du réseau comme sélection. Il calcule trois mesures centrales pour chaque ligne du réseau dont la valeur est supérieure au seuil fixé (degree_thresh, closeness_thresh et betweeness_thresh). Si les trois seuils sont fixés, alors la sélection portera sur les lignes qui correspondent aux trois seuils.
  
  

Généralisation par le déplacement

• Displacement: Cet algorithme est utilisé lorsque les lignes se chevauchent ou sont trop proches les unes des autres. En général, les méthodes de déplacement décalent les objets conflictuels afin qu'ils n'interagissent pas et qu’ils puissent être distingués. Cette méthode est basée sur l’algorithme du serpent (Snake). Elle a de très bons résultats mais nécessite beaucoup de mémoire, ce qui fait qu’elle n’est pas très efficace. Pour l’utiliser il faut renseigner les paramètres threshold (seuil), alpha, beta et iterations (nombre d'itérations) (dont la valeur doit être comprise entre 10 et 100 pour de bons résultats).
  
  
  

Description des différents paramètres :

input=name Nom de la couche vecteur en entrée

output=name Nom de la couche vecteur en sortie

type=string[,string,…] Type d'objets à généraliser
Par défaut : line (lignes),boundary (contour),area (surface)

method=string Choix de l’algorithme à utiliser pour la généralisation de la couche (description faite ci-dessus)
Par défaut :douglas

threshold=float Valeur de tolérance maximale
Options: 0-1 000 000 000
Par défaut : 1.0

look_ahead=integer
Par défaut : 7

reduction=float Pourcentage de points dans la couche vecteur en sortie avec « douglas_reduction »
Options: 0-100
Par défaut : 50

slide=float Décalage des points calculés par rapport au point original
Options: 0-1
Par défaut : 0.5

angle_thresh=float Angle minimum entre deux segments consecutive dans l’algorithme Hermite
Options: 0-180
Par défaut : 3

degree_thresh=integer
Degrée seuil utilisé dans l'algorithme network generalization
Par défaut : 0

closeness_thresh=float Seuil de proximité dans l’algorithme network
Options: 0-1
Par défaut : 0

betweeness_thresh=float
Seuil de Betweeness dans l’algorithme network
Par défaut : 0

alpha=float Paramètre alpha dans l’algorithme Snakes
Par défaut : 1.0

beta=float Paramètre beta dans l’algorithme Snakes
Par défaut : 1.0

iterations=integer Nombre d’itérations
Par défaut : 1

— Remis à jour par Sophie Mollard 2015/01/19 20:10