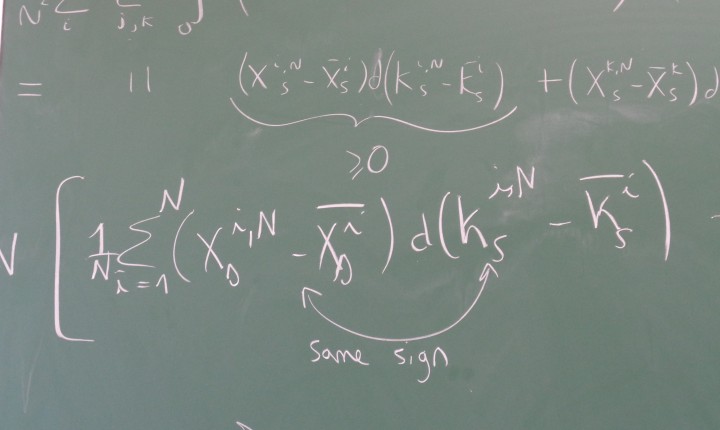Nonlinear Processes and their Applications

Workshop Institut Camille Jordan

 Aim of the workshop

     The particularity of the nonlinear processes is that they satisfy some stochastic differential equations where there is no linearity (with respect to the associated partial differential equation). The linear stochastic processes had been well known for decades. But, the nonlinear ones are the subject of intense researchs in the domain of the probability, in the partial differential equations but also in the applications of the mathematics. However, real phenomena are more often nonlinear processes than linear one. Let us give some examples of nonlinear processes that we are interested in:

  The self-stabilizing diffusion. This diffusion can be obtained as a limit of mean-field particles interacting system. It has been initially constructed to modelize the plasmas. However, it now is used to study chemical or biological species in interaction or in the contraction of the muscular cells.

The diffusion of Dreyer et al. This diffusion is of McKean-Vlasov type. It is used to count the proportion of Lithium atoms in a Lithium-battery. By assuming that the charge is slow, an hysteresis phenomenon appears. Nevertheless, this phenomenon (obtained by some authors by analytical techniques) is not well understood in the probabilistic view point.

The Delarue Inglis Rubenthaler and Tanré diffusion. It is used to modelise the potential of the membrane of a neuron in a neuronal system with a large number of neurons. Some metastability questions occurs for this model which well-posedness has been obtained in 2015.

The self-interacting diffusion. In addition to its use to modelise some polymers, it can also be used in stochastic algorithms. Indeed, the classical method of gradient descending has a default: the slowness if the cost potential that we search the minimum (which is classical when we do a maximum of likelihood) is nonconvex. So, we used the simulated anneahiling. By using the self-interacting diffusion, one expect to reduce the exit-time so that the method would be faster.

The Cucker-Smale diffusion. This diffusion is a stochastic version of the classical Cucker-Smale model. This model is used to understand the flocking. It is of McKean-Vlasov type with also the position.

Organizing committee

Romain Ravaille, Institut Camille Jordan
Julian Tugaut, Institut Camille Jordan
Pascale Villet, Institut Camille Jordan

 List of confirmed speakers

• Alessandra BIANCHI, Padova (Italy)
• Paul-Eric CHAUDRU DE RAYNAL, Chambéry (France)
• François DELARUE, Nice (France)
• Gonçalo DOS REIS, Edinburgh (United Kingdom)
• Hong DUONG, Birmingham (United Kingdom)
• Jean-François JABIR, Moscow (Russia)
• Aline KURTZMANN, Nancy (France)
• Michela OTTOBRE, Edinburgh (United Kingdom)
• Grigorios PAVLIOTIS, London (United Kingdom)
• Lukasz SZPRUCH, Edinburgh (United Kingdom)
• Etienne TANRÉ, Nice (France)
• Milica TOMASEVIC, Polytechnique (France)

 Program

Workshop schedule
Workshop program

Poster session

• Oumaima BENCHEIKH, (École des Ponts ParisTech)
• Quentin CORMIER (Nice):
• Paul DOBSON (Edinburgh):
• William HAMMERSLEY (Edinburgh):
• Romain RAVAILLE (Saint-Étienne):
• William SALKELD (Edinburgh):

Slides

To be announced soon

Inscription

For your registration, please click  HERE  before the deadline : June 21st
Registrations are now closed.

 Practical informations

• Except for the speakers, you must pay the lunch.
• The talks will take place in the Faculty of Sciences, room A 14, 23 rue du Docteur Paul Michelon, Saint-Étienne
• Venue: Address: Institut Camille Jordan, Faculté des Sciences et Techniques, 23 rue du Docteur Paul Michelon, 42023 Saint-Étienne Cedex 2
• How to arrive from Aeroport Lyon Saint-Exupery: The shuttle Ouibus makes the connection form Lyon Saint-Exupery airport to Saint-Etienne main train station.
  And by Rhône-express (https://www.rhonexpress.fr/) + train (TER Lyon Part Dieu-Saint-Etienne: (https://www.ter.sncf.com/auvergne-rhone-alpes)
• How to arrive from Lyon-Part Dieu or Lyon-Perrache: By train, https://www.ter.sncf.com/auvergne-rhone-alpes (TER journeys to/from Saint-Etienne and Lyon take under 50 minutes).
• How to go from the main station Saint-Etienne Chateaucreux to the Institute Camille Jordan:
  The city bus company: STAS: http://www.reseau-stas.fr/fr/itineraires/4/JourneyPlannerThe Bus line M4 takes you from the main train station (Saint-Etienne Châteaucreux) to the faculty of Sciences.
  And bus line M6  takes you from the heart of the city, square Violette, to the faculty.
• Stay : You will find HERE a selection of hotels in the center of the city.

Poster of the workshop : HERE