Nineth International Workshop on the Multiscale Modeling and Methods
Le 4 juin 2019
Faculty of Sciences and Technologies
(Salle du conseil)
Organised by the Federative Research Structure MODMAD and the Camille Jordan Institute
Nineth International Workshop
on the Multiscale Modeling and Methods
Saint-Etienne, June 4, 2019
The multiscale analysis of heterogeneous structures is actually an effective tool of mathematical modeling in physics, technique and biology. There are important open problems in constructing realistic models of new materials and engineering structures, biological processes, especially combining different scales or discrete and continuous approaches. The workshop is the nineth event in the set yearly-organized international conferences or workshops on the multiscale methods and modeling. The first three and the sixth were held at the University of Saint-Etienne, France. The fourth and the fifth were held in Moscow, at the Institute of Numerical Mathematics of Russian Academy of Sciences (RAS) in October 2014 and at the Bauman Moscow State Technical University in June 2015. Both were organized in the frame of the thematic year on the multiscale methods and modeling in biology and medicine organized by the Russian-French research center J.-V.Poncelet. The seventh and the eighth conferences were held in the frame of the thematic year on the multiscale modeling in biology at the University of Chile and organized by the French-Chilian laboratory CMM (Center for Mathematical Modeling) http://eventos.cmm.uchile.cl/multiscale2018. The present workshop will be devoted mainly to the mathematical issues in multi-scale analysis, in particular, to the spectral properties of multiscale models related to so called frequency dependent materials. The application of these methods allows constructing new materials with given properties, creating new more adequate and more precise models in material science. That is why this year the workshop is associated to and is organized just one day before the workshop of GDR MORPHEA http://gdr-morphea.cnrs.fr
Organizer:
Grigory Panasenko, Saint-Etienne, France
Preliminary list of speakers :
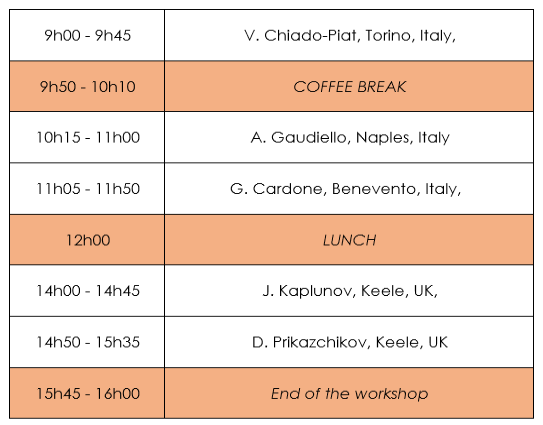
- G. Cardone, Benevento, Italy,
- V. Chiado-Piat, Torino, Italy,
- A. Gaudiello, Naples, Italy
- J. Kaplunov, Keele, UK,
- D. Prikazchikov, Keele, UK
Program
Abstracts
G. Cardone
Title: Norm-resolvent convergence for elliptic operators in a planar waveguide perforated along a curve
Abstract: We consider an infinite planar straight strip perforated by small holes along a curve.
In such a domain, we consider a general second-order elliptic operator subject to classical boundary conditions on the holes. Assuming that the perforation is non-periodic and satisfies rather weak assumptions, we describe all possible homogenized problems. Our main result is the norm-resolvent convergence of the perturbed operator to a homogenized one in various operator norms and the estimates for the rate of convergence. On the basis of the norm-resolvent convergence, we prove the convergence of the spectrum.
The results are obtained in a joint paper with D.Borisov (Ufa, Russia) and T.Durante (Salerno, Italy).
V. Chiado-Piat
Title: Homogenization of some quasi-linear elliptic equations with gradient constraints
Abstract: We discuss a homogenization formula for quasi-linear elliptic equations with gradient constraints on a disperse set, within the framework of monotonic operator theory and compensated compactness methods.
This is a joint work with M.Zoboli.
A. Gaudiello
Title: Homogenization of a nonlinear monotone problem with nonlinear Signorini boundary conditions in a domain with highly rough boundary.
Abstract: This talk is based on joined works with Taras Mel'nyk of National Taras Shevchenko University of Kyiv (Ukraine). A domain $\Omega_\varepsilon\subset \mathbb{R}^N$, $N\geq2$, with a very rough boundary depending on $\varepsilon$ is introduced. For instance, if $N=3$ $\Omega_\varepsilon$ has the form of a brush with an $\varepsilon$-periodic distribution of thin cylindrical teeth with fixed height and a small diameter of order $\varepsilon$. In $\Omega_\varepsilon$, a nonlinear monotone problem with nonlinear Signorini boundary conditions, depending on $\varepsilon$, on the lateral boundary of the teeth is considered. The asymptotic behavior of this problem, as $\varepsilon$ vanishes, i.e. when the number of thin attached cylinders increases unboundedly while their cross sections tend to zero, is studied. The limit problem which is a nonstandard homogenized problem is identified.
J. Kaplunov
Title: On similarity of multiscale procedures for thin and periodic structures
Abstract: A similarity between two-scale asymptotic procedures for thin and periodic structures is addressed, e.g. see [1]. For each of the approaches a macroscale wave length is assumed to be much greater than a microscale size corresponding to a typical linear dimension of a periodicity cell or transverse thickness. Both low- and high-frequency regimes are analysed. In particular, the so-called long-wave high-frequency approximation for elastic plates and shells [2], is considered to be a counterpart of the high-frequency homogenisatıon scheme for periodic media [3]. The latter is mostly oriented to analysis of micro-scale dynamic phenomena and finds important applications in modelling of meta-materials.
References
1. Craster, R. V., Joseph, L. M., & Kaplunov, J. (2014). Long-wave asymptotic theories: the connection between functionally graded waveguides and periodic media. Wave Motion, 51(4), 581-588.
2. Kaplunov, J. D., Kossovitch, L. Y., & Nolde, E. V. (1998). Dynamics of thin walled elastic bodies. Academic Press.
3. Craster, R. V., Kaplunov, J., & Pichugin, A. V. (2010). High-frequency homogenization for periodic media. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 466(2120), 2341-2362.
D. Prikazchikov
Title: Low-frequency vibrations of strongly inhomogeneous layered elastic plates
Abstract: Low-frequency vibrations of strongly inhomogeneous elastic plates are subject to multiparametric asymptotic analysis, see [1,2] for more detail. The focus is on several practically motivated examples of two- and three-layered structures, for which the lowest thickness resonances are close to zero. In this case, the associated spectra relations exhibit extra low-frequency branch instead of a single bending one typical of a homogeneous thin Kirchhoff plate. Two-mode low-frequency asymptotic models for a three-layered plate are analysed, including both uniform and non-uniform approximations of the original 3D equations in linear elastodynamics. Numerical comparisons of exact and approximate results are presented.
References
1. Kaplunov, J., Prikazchikov, D. A., & Prikazchikova, L. A. (2017). Dispersion of elastic waves in a strongly inhomogeneous three-layered plate. International Journal of Solids and Structures, 113, 169-179.
2. Prikazchikova, L., Ece Aydın, Y., Erbaş, B., & Kaplunov, J. (2018). Asymptotic analysis of an anti-plane dynamic problem for a three-layered strongly inhomogeneous laminate. Mathematics and Mechanics of Solids, doi: 1081286518790804.
Registration
Registration are closed
Deadline for registration : May 19, 2019
Poster of the workshop : HERE




Grigory PANASENKO
grigory.panasenko @ univ-st-etienne.fr
Localisation